Geometric Understanding of Sketches
Raghav BV's Ph.D. Thesis
(PDF) (PDF-compressed) (arXiv)
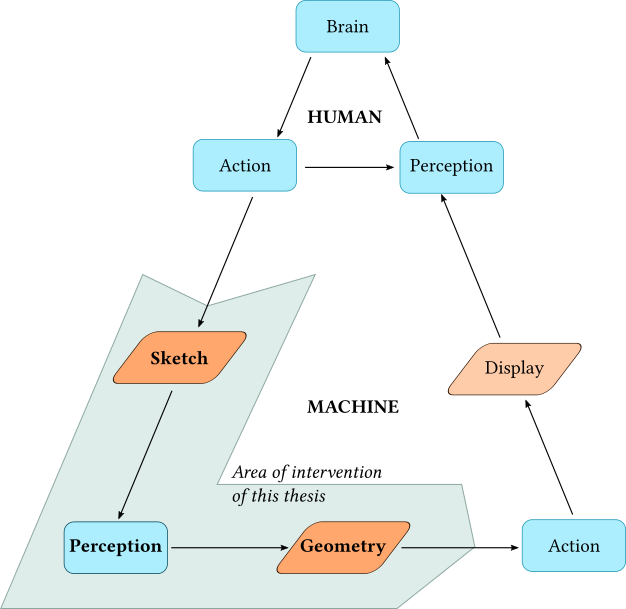
Figure 1: The feedback loop of sketching as an exercise.
- How to cite
@phdthesis{Ven22, address = {Kanpur}, type = {Ph.{D}. {Thesis}}, title = {Geometric Understanding of Sketches}, language = {EN}, school = {IIT Kanpur}, author = {Venkataramaiyer, Raghav Brahmadesam}, month = March, year = {2022}, }
- Abstract
Sketching is used as a ubiquitous tool of expression by novices and experts alike. In this thesis I explore two methods that help a system provide a geometric machine-understanding of sketches, and in-turn help a user accomplish a downstream task.
The first work deals with interpretation of a 2D-line drawing as a graph structure, and also illustrates its effectiveness through its physical reconstruction by a robot. We setup a two-step pipeline to solve the problem. Formerly, we estimate the vertices of the graph with sub-pixel level accuracy. We achieve this using a combination of deep convolutional neural networks learned under a supervised setting for pixel-level estimation followed by the connected component analysis for clustering. Later we follow it up with a feedback-loop-based edge estimation method. To complement the graph-interpretation, we further perform data-interchange to a robot legible ASCII format, and thus teach a robot to replicate a line drawing.
In the second work, we test the 3D-geometric understanding of a sketch-based system without explicit access to the information about 3D-geometry. The objective is to complete a contour-like sketch of a 3D-object, with illumination and texture information. We propose a data-driven approach to learn a conditional distribution modelled as deep convolutional neural networks to be trained under an adversarial setting; and we validate it against a human-in-the-loop. The method itself is further supported by synthetic data generation using constructive solid geometry following a standard graphics pipeline. In order to validate the efficacy of our method, we design a user-interface plugged into a popular sketch-based workflow, and setup a simple task-based exercise, for an artist. Thereafter, we also discover that form-exploration is an additional utility of our application.
Using the two methods, validated against a real-world setup, we set a precedent for an arguably robust machine understanding of geometric forms expressed as sketches, in the former for 2D geometry in the context of a robot-based task, and in the latter for 3D geometry in the live context of a sketch-completion task.
Updated 2022-05-28 Sat 13:40 BST